Specialspel och uträkningarna
Senast så tog jag upp hur man räknar ut det matematiskt korrekta oddset för en viss specialare. Jag fick lite frågor om detta, den vanligaste var att jag enbart räknade det det exakta målantalet för den första matchen. Detta gör jag för att förenkla uträkningen och jag tänkte göra ett exempel för att förklara bättre.
Hämta Expekts Freebet på 100% upp till 1500kr här!
Om du slår två sexsidiga tärningar så finns kommer det hamna på 2-12 ihopräknat, men hur stor är chansen att det hamnar på ö8,5 på dessa?
Om vi slår bägge tärningarna samtidigt så finns det exakt 36 utfall (6×6). Men skriver du upp alla enskilda så är det (3+6, 4+5, 4+6, 5+4, 5+5, 5+6, 6+3, 6+4, 6+5, 6+6) tio (10) som blir ö8,5 totalt. Det blir en sannolikhet på 10/36, ca 28% att du slår detta.
På detta sätt behöver vi räkna ut sannolikheter för varje enskilt utfall, vilket kan bli stökigt vad gäller odds på olika mängder mål tex. Men vi kan även ställa upp det på ett sätt där vi tänker att vi slår en tärning i taget och sannolikheten att slå nio eller högre beror på första slaget. Det finns sex olika utfall på första tärningen med samma sannolikhet.
Sannolikheterna blir då beroende på vad du slår:
1. 1 / 6 * 0 = 0. Sannolikheten för att slå en etta är 1 / 6. Sedan över ö7,5 är noll chans, därför blir denna sannolikhet totalt noll.
2. 1 / 6 * 0 = 0. Sannolikheten för att slå en tvåa är 1 / 6. Sedan över ö6,5 är noll chans, därför blir denna sannolikhet totalt noll.
3. 1 / 6 * 1 / 6 = 1 / 36. Sannolikheten för att slå en trea är 1 / 6. Sedan över ö5,5 är 1 / 6, därför blir denna sannolikhet totalt 1 / 36.
4. 1 / 6 * 2 / 6 = 2 / 36. Sannolikheten för att slå en fyra är 1 / 6. Sedan över ö4,5 är 2 / 6, därför blir denna sannolikhet totalt 2 / 36.
5. 1 / 6 * 3 / 6 = 3 / 36. Sannolikheten för att slå en femma är 1 / 6. Sedan över ö3,5 är 3 / 6, därför blir denna sannolikhet totalt 3 / 36.
6. 1 / 6 * 4 / 6 = 4 / 36. Sannolikheten för att slå en sexa är 1 / 6. Sedan över ö2,5 är 4 / 6, därför blir denna sannolikhet totalt 4 / 36.
Adderar vi sedan dessa sannolikheter så blir det (1 / 36 + 2 / 36 + 3 / 36 + 4 / 36) återigen 10/36. Ca 28% och ett odds på 3,6 ggr pengarna.
Vi applicerar det på Expekts senaste specialare:
Vi sätter upp det liksom med tärningarna att matcherna spelas efter varandra. Första matchen har återigen sex olika utfall:
1. Arsenal gör noll mål. Då måste PSG göra ö4,5 mål.
2. Arsenal gör ett mål. Då måste PSG göra ö3,5 mål.
3. Arsenal gör två mål. Då måste PSG göra ö2,5 mål.
4. Arsenal gör tre mål. Då måste PSG göra ö1,5 mål.
5. Arsenal gör fyra mål. Då måste PSG göra ö0,5 mål.
6. Arsenal gör fem eller fler mål. Då behöver inte PSG göra ngt mål.
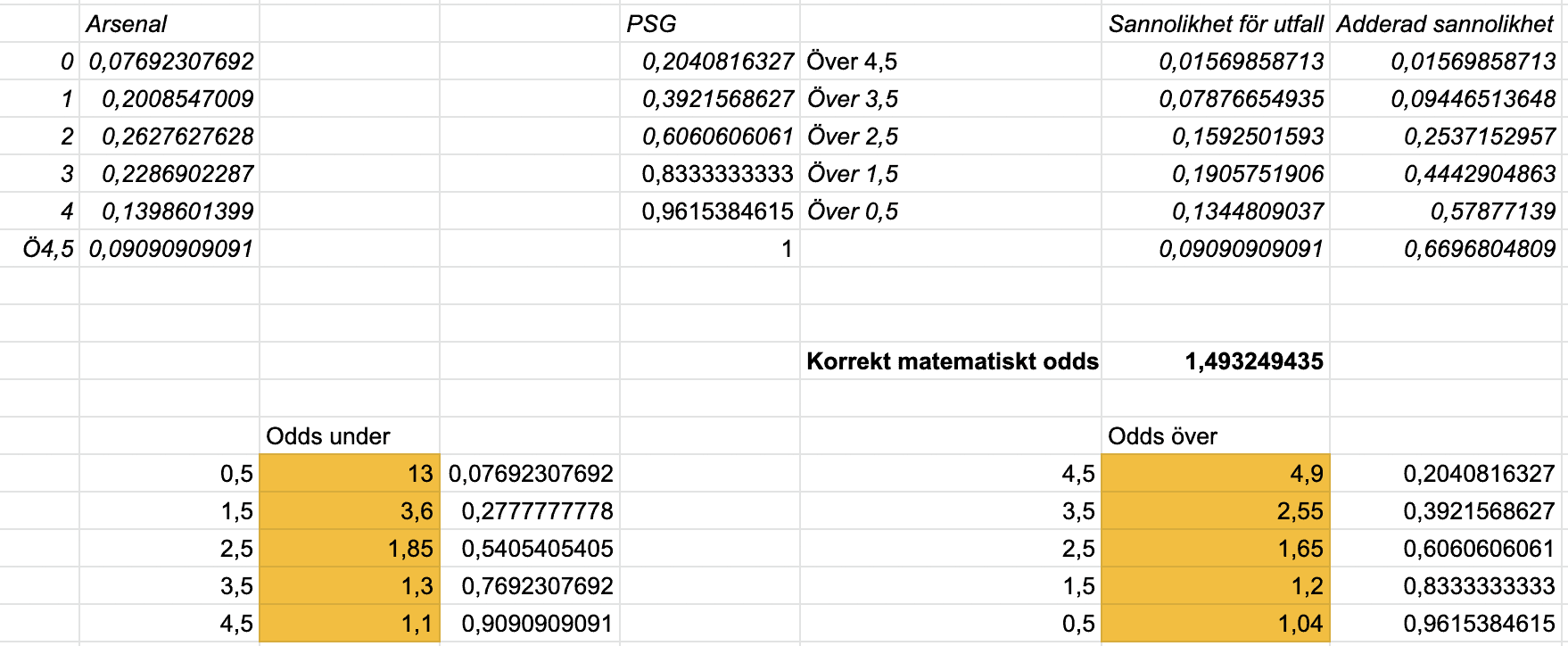
Vi använder formeln från förra inlägget (se inlägget här) och räknar ut sannolikheten för Arsenals exakta mål och oddsen för att PSG ska göra över ett visst antal mål:
1. 0,077 * 0,204 = 0,0157
2. 0,20 * 0,392 = 0,079
3. 0,263 * 0,606 = 0,159
4. 0,229 * 0,833 = 0,191
5. 0,140 * 0,962 = 0,134
6. 0,091 * 1 = 0,091
Adderade sannolikheterna blir då 0,6697 vilket motsvarar ett odds på 1,493. Specialaren ger ett odds på 1,70 och vi får ett rejält värde på spelet.
Bifogar uträkningen i Excel, har vi en gång ställt upp det så behöver vi enbart fylla i de gula rutorna med lagens odds för mål.
Jag kommer fortsätta ta upp fler av dessa och räkna på rent matematiska spel. Hör gärna av er om frågor och om det är något speciellt ni vill att jag ska ta upp.
Hämta Expekts Freebet på 100% upp till 1500kr här!
Lycka till med era specialspel!




